"스털링 공식"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
(피타고라스님이 이 페이지에 3140469 파일을 등록하셨습니다.)
 
(사용자 2명의 중간 판 25개는 보이지 않습니다)
1번째 줄: 1번째 줄:
−
<h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">이 항목의 스프링노트 원문주소</h5>
+
==개요==
  
−
* [[스털링 공식]]
+
* [[팩토리얼(factorial)]]의 근사식 :<math> n! \approx \sqrt{2\pi n}\, \left(\frac{n}{e}\right)^{n}</math>
 +
* 좀더 정확한 [[점근 급수(asymptotic series)]]는 다음과 같이 주어짐 :<math>  n!=\sqrt{2\pi n}\left({n\over e}\right)^n  \left(    1    +{1\over12n}    +{1\over288n^2}    -{139\over51840n^3}    -{571\over2488320n^4}    + \cdots  \right)</math>
  
−
 
+
==증명1 : 오일러-맥클로린 공식의 응용==
  
−
 
+
*  먼저 <math>n!</math> 에 로그를 취하여 덧셈형태로 쓴다:<math>\ln(n!)= \sum_{k = 0}^{n-1}\ln(1+k)</math>
 +
* 이제 [[오일러-맥클로린 공식]]을 사용하자.
 +
:<math>\sum_{i=0}^{n-1} f(i) = \sum_{k=0}^p\frac{B_k}{k!}\left(f^{(k-1)}(n)-f^{(k-1)}(0)\right)+R</math>
 +
* 다시쓰면,
 +
:<math>\sum_{i=0}^{n-1} f(i) = \int^n_0f(x)\,dx-\frac{1}{2}(f(n)-f(0))+\frac{1}{12}(f'(n)-f'(0))-\frac{1}{720}(f^{(3)}(n)-f^{(3)}(0))+\frac{1}{30240}(f^{(5)}(n)-f^{(5)}(0))-\frac{1}{1209600}(f^{(7)}(n)-f^{(7)}(0))+\cdots</math>
 +
* 오차항은 다음과 같이 주어짐
 +
:<math>\left|R\right|\leq\frac{2}{(2\pi)^{2(p+1)}}\int_0^n\left|f^{(p)}(x)\right|\,dx</math>
 +
* <math>f(x) = \ln(1+x)</math> 에서 유도. <math>R</math> 은 0 으로 수렴한다.
 +
:<math>f^{(k-1)}(x)=(-1)^{k-1}\frac{(k-1)!}{x^{k}}</math>
 +
:<math>\frac{B_k}{k!}\left(f^{(k-1)}(n)-f^{(k-1)}(1)\right) =(-1)^{k-1}\frac{B_k}{k}(\frac{1}{n^{k}}-1)</math>
 +
:<math>\int f(x)\,dx=(1+x)\ln (1+x)-x</math>
 +
:<math>f(x)=\ln (1+x)</math>
 +
:<math>f'(x)=\frac{1}{1+x}</math>
 +
:<math>f^{(2)}(x)=\frac{-1}{(1+x)^2}</math>
 +
:<math>f^{(3)}(x)=\frac{2}{(1+x)^3}</math>
 +
:<math>f^{(4)}(x)=\frac{-6}{(1+x)^4}</math>
 +
:<math>f^{(k-1)}(x)=(-1)^{k}\frac{(k-1)!}{x^{k-1}}</math>
  
−
<h5>개요</h5>
+
* 위의 결과를 쓰면
 +
:<math>\ln(n!)= \sum_{k = 0}^{n-1}\ln(1+k)=n\ln n - n-\frac{1}{2}\ln n+\frac{1}{12}(\frac{1}{n}-1)+\cdots</math>
  
−
* 팩토리얼의 근사식
+
그러므로,
−
 
+
:<math> n! \approx B\sqrt{n}\, \left(\frac{n}{e}\right)^{n}</math>
−
<math> n! \approx \sqrt{2\pi n}\, \left(\frac{n}{e}\right)^{n}</math>
+
*  계수 <math>\sqrt{2 \pi}</math> 는 어떻게 얻을까?
−
 
+
** [[월리스 곱 (Wallis product formula)|월리스 곱]]을 이용할 수 있다.
−
*  좀더 정확히는 다음과 같이 주어짐.<br><math> n!=\sqrt{2\pi n}\left({n\over e}\right)^n   \left(    1    +{1\over12n}   +{1\over288n^2}   -{139\over51840n^3}   -{571\over2488320n^4}   + \cdots  \right)</math><br>
+
:<math>\frac{\pi}{2}=\lim_{n\to\infty}{1\over{2n}}\cdot{{2^{4n}\,(n!)^4}\over{((2n)!)^2}}</math>
−
 
+
:<math>\sqrt{\frac{\pi}{2}}=\lim_{n\to\infty}\sqrt{{1\over{2n}}}\cdot{{2^{2n}\,(n!)^2}\over{(2n)!}}=\lim_{n\to\infty}\sqrt{{1\over{2n}}}\cdot{{2^{2n}\,(B\sqrt{n}\, \left(\frac{n}{e}\right)^{n})^2}\over{B\sqrt{2n}\, \left(\frac{2n}{e}\right)^{2n}}}=\frac{B}{2}</math>
−
 
+
따라서
−
 
+
:<math>B=\sqrt{2\pi}</math>
−
<h5>증명</h5>
 
−
 
 
−
*  먼저 <math>n!</math> 에 로그를 취하여 덧셈형태로 쓴다<br><math>\ln(n!)= \sum_{k = 0}^{n-1}\ln(1+k)</math><br>
 
−
* 이제 [[오일러-맥클로린 공식|http://pythagoras0.springnote.com/pages/2637804]]을 사용하자.
 
  
−
 
+
==증명2: 안장점 근사의 응용==
  
−
<math>\sum_{i=0}^{n-1} f(i) = \sum_{k=0}^p\frac{B_k}{k!}\left(f^{(k-1)}(n)-f^{(k-1)}(0)\right)+R</math>
+
* [[안장점 근사]]
 +
*  일반적으로 N이 클 때, 다음과 같은 근사식이 성립한다 :<math>\int e^{Nf(x)}\,dx\approx \sqrt{\frac{2\pi}{N|f''(x_0)|}}e^{Nf(x_0)}\textrm{ as }N\to\infty</math> 최대값 부근에서의 테일러 전개 <math>f(x)\approx f(x_0)-\frac{1}{2}|f''(x_0)|(x-x_0)^2</math>를 이용
 +
* 스털링공식에의 적용
  
−
<math>\sum_{i=0}^{n-1} f(i) = \int^n_0f(x)\,dx-\frac{1}{2}(f(n)-f(0))+\frac{1}{12}(f'(n)-f'(0))-\frac{1}{720}(f^{(3)}(n)-f^{(3)}(0))+\frac{1}{30240}(f^{(5)}(n)-f^{(5)}(0))-\frac{1}{1209600}(f^{(7)}(n)-f^{(7)}(0))+\cdots</math>
+
  
−
오차항은  <math>\left|R\right|\leq\frac{2}{(2\pi)^{2(p+1)}}\int_0^n\left|f^{(p)}(x)\right|\,dx</math> 로 주어짐.
+
<math>N! = \Gamma(N+1)=\int_0^{\infty} e^{-x} x^N dx</math> 에서 <math>x=Nz</math> 로 치환하면,
  
−
* <math>f(x) = \ln(1+x)</math> 에서 유도. <math>R</math> 은 0 으로 수렴한다.<br><math>f^{(k-1)}(x)=(-1)^{k-1}\frac{(k-1)!}{x^{k}}</math>
+
<math>N!= \int_0^{\infty} e^{-N z} \left(N z \right)^N N dz=N^{N+1}\int_0^{\infty}e^{N(\ln z-z)} dz</math>
  
−
<math>\frac{B_k}{k!}\left(f^{(k-1)}(n)-f^{(k-1)}(1)\right) =(-1)^{k-1}\frac{B_k}{k}(\frac{1}{n^{k}}-1)</math>
+
<math>f \left( z \right) = \ln{z}-z</math>
  
−
<math>\int f(x)\,dx=(1+x)\ln (1+x)-x</math>, <math>f(x)=\ln (1+x)</math>, <math>f'(x)=\frac{1}{1+x}</math>,  <math>f^{(2)}(x)=\frac{-1}{(1+x)^2}</math>, <math>f^{(3)}(x)=\frac{2}{(1+x)^3}</math>,  <math>f^{(4)}(x)=\frac{-6}{(1+x)^4}</math>, <math>f^{(k-1)}(x)=(-1)^{k}\frac{(k-1)!}{x^{k-1}}</math>
+
<math>f'(z) = \frac{1}{z}-1</math>
  
−
* 위의 결과를 쓰면
+
<math>f''(z) = -\frac{1}{z^2}</math>
  
−
<math>\ln(n!)= \sum_{k = 0}^{n-1}\ln(1+k)=(n+1)\ln (n+1) - n-\frac{1}{2}\ln(n+1)+\frac{1}{12}(\frac{1}{1+n}-1)+\cdots</math>
+
<math>z_0=1</math> 일 때, 최대값을 가지며, <math>f(z)\approx -1-\frac{1}{2} (z-1)^2+O[z-1]^3</math> 가 된다.
  
−
그러므로,
+
따라서
  
−
<math> n! \approx B\sqrt{n}\, \left(\frac{n}{e}\right)^{n}</math>
+
<math>N! \approx N^{N+1}\int_0^{\infty}e^{-N}e^{-\frac{N(z-1)^2}{2}} dz \approx N^{N+1}\sqrt{\frac{2\pi}{N}} e^{-N}=\sqrt{2\pi N} N^N e^{-N}</math>
  
−
* 계수 <math>\sqrt{2 \pi}</math> 는 어떻게 얻을까?<br>
+
   
−
** [[월리스 곱 (Wallis product formula)|월리스 곱]]을 이용할 수 있다.
 
  
−
<math>\frac{\pi}{2}=\lim_{n\to\infty}{1\over{2n}}\cdot{{2^{4n}\,(n!)^4}\over{((2n)!)^2}}</math>
+
N=100일 때,
  
−
<math>\sqrt{\frac{\pi}{2}}=\lim_{n\to\infty}\sqrt{{1\over{2n}}}\cdot{{2^{2n}\,(n!)^2}\over{(2n)!}}=\lim_{n\to\infty}\sqrt{{1\over{2n}}}\cdot{{2^{2n}\,(B\sqrt{n}\, \left(\frac{n}{e}\right)^{n})^2}\over{B\sqrt{2n}\, \left(\frac{2n}{e}\right)^{2n}}}=\frac{B}{2}</math>
+
<math>\sqrt{\frac{2\pi}{N}} e^{-N}\approx 9.33262\times 10^{-45}</math>
  
−
<math>B=\sqrt{2\pi}</math>
+
<math>\int_0^{\infty}e^{N(\ln z-z)} dz\approx 9.32485\times 10^{-45}</math>
  
−
 
+
  
−
 
+
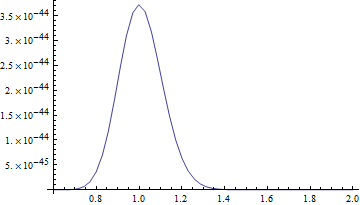
<math>e^{N(\ln z-z)}</math> 의 그래프
 +
[[파일:스털링 공식1.gif]]
  
−
<h5>안장점 근사를 이용한 증명</h5>
+
  
−
 
 
  
−
 
+
==재미있는 사실==
  
−
 
+
*  드무아브르가 스털링에 앞서서 팩토리얼의 근사식을 유도함.
−
 
+
*  다만 <math>\sqrt{2\pi}</math>이라는 상수를 구하지 않고 적당한 상수 <math>B</math>에 대하여 다음과 수준의 표현을 남김.:<math> n! \approx B\sqrt{n}\, \left(\frac{n}{e}\right)^{n}</math>
−
<h5>재미있는 사실</h5>
+
*  나중에 <math>B=\sqrt{2\pi}</math> 는 스털링이 해결함.
−
 
 
−
*  드무아브르가 스털링에 앞서서 팩토리얼의 근사식을 유도함.<br>
 
−
*  다만 <math>\sqrt{2\pi}</math>이라는 상수를 구하지 않고 적당한 상수 <math>B</math>에 대하여 다음과 수준의 표현을 남김.<br><math> n! \approx B\sqrt{n}\, \left(\frac{n}{e}\right)^{n}</math><br>
 
−
*  나중에 <math>B=\sqrt{2\pi}</math> 는 스털링이 해결함.<br>
 
−
 
 
−
* [http://www-groups.dcs.st-and.ac.uk/%7Ehistory/Biographies/De_Moivre.html 역사는 다음과 같은 이야기]를 전한다.<br>
 
  
 
<blockquote style="line-height: 2em; margin: 0px; padding: 0px 0px 0px 38px; background-color: rgb(239, 239, 239); background-position: 14px 4px;">
 
<blockquote style="line-height: 2em; margin: 0px; padding: 0px 0px 0px 38px; background-color: rgb(239, 239, 239); background-position: 14px 4px;">
 
In Miscellanea Analytica (1730) appears Stirling’s formula (wrongly attributed to Stirling) which de Moivre used in 1733 to derive the normal curve as an approximation to the binomial. In the second edition of the book in 1738 de Moivre gives credit to Stirling for an improvement to the formula. De Moivre wrote:-
 
In Miscellanea Analytica (1730) appears Stirling’s formula (wrongly attributed to Stirling) which de Moivre used in 1733 to derive the normal curve as an approximation to the binomial. In the second edition of the book in 1738 de Moivre gives credit to Stirling for an improvement to the formula. De Moivre wrote:-
  
−
'''I desisted in proceeding farther till my worthy and learned friend Mr James Stirling, who had applied after me to that inquiry, [discovered that c = √(2 π)].'''
+
'''I desisted in proceeding farther till my worthy and learned friend Mr James Stirling, who had applied after me to that inquiry, [discovered that c = √(2 π)].''' ([http://www-groups.dcs.st-and.ac.uk/%7Ehistory/Biographies/De_Moivre.html http://www-groups.dcs.st-and.ac.uk/~history/Biographies/De_Moivre.html])
 
</blockquote>
 
</blockquote>
  
−
*  오늘날 팩토리얼의 근사식은 선구적인 업적을 남긴 드무아브르의 이름은 온데간데 없이 스털링의 공식이라고 불리게 됨.<br>
+
*  오늘날 팩토리얼의 근사식은 선구적인 업적을 남긴 드무아브르의 이름은 온데간데 없이 스털링의 공식이라고 불리게 됨.
−
*  드무아브르는 조금 섭섭하지 않을런지?<br>
+
*  드무아브르는 조금 섭섭하지 않을런지?
−
*  팩토리얼은 정의는 간단할지라도 n이 조금만 커지기 시작하면 계산하기가 그리 만만치 않음. 실용적인 측면에서도 유용한 근사식.<br>
+
*  팩토리얼은 정의는 간단할지라도 n이 조금만 커지기 시작하면 계산하기가 그리 만만치 않음. 실용적인 측면에서도 유용한 근사식.
  
−
 
+
  
−
<h5>관련된 단원</h5>
+
  
−
 
+
  
−
 
+
==관련된 항목들==
−
 
 
−
<h5>많이 나오는 질문</h5>
 
−
 
 
−
*  네이버 지식인<br>
 
−
** http://kin.search.naver.com/search.naver?where=kin_qna&query=
 
−
 
 
−
 
 
−
 
 
−
<h5>관련된 고교수학 또는 대학수학</h5>
 
−
 
 
−
* [[오일러-맥클로린 공식]]<br>  <br>
 
−
 
 
−
 
 
−
 
 
−
<h5>관련된 다른 주제들</h5>
 
  
 
* [[감마함수]]
 
* [[감마함수]]
 
* [[월리스 곱 (Wallis product formula)|월리스 곱]]
 
* [[월리스 곱 (Wallis product formula)|월리스 곱]]
 
* [[파이가 아니라 2파이다?]]
 
* [[파이가 아니라 2파이다?]]
 +
* [[오일러-맥클로린 공식]]
 +
* [[가우시안 적분]]
  
−
 
 
  
−
<h5>관련도서 및 추천도서</h5>
+
==매스매티카 파일 및 계산 리소스==
 +
* https://docs.google.com/file/d/0B8XXo8Tve1cxM1A5QS1rMkkwbUE/edit
  
−
*  도서내검색<br>
+
==수학용어번역==
−
** http://books.google.com/books?q=
+
* {{학술용어집|url=asymptotic}}
−
** http://book.daum.net/search/contentSearch.do?query=
 
−
*  도서검색<br>
 
−
** http://www.amazon.com/s/ref=nb_ss_gw?url=search-alias%3Dstripbooks&field-keywords=
 
−
** http://book.daum.net/search/mainSearch.do?query=
 
  
−
 
+
==사전형태의 자료==
  
−
<h5>참고할만한 자료</h5>
 
−
 
−
* [http://www.jstor.org/stable/2324749 A New Derivation of Stirling's Approximation to n!]<br>
 
−
** George Marsaglia and John C. W. Marsaglia, The American Mathematical Monthly, Vol. 97, No. 9 (Nov., 1990), pp. 826-829
 
 
* [http://ko.wikipedia.org/wiki/%EC%8A%A4%ED%84%B8%EB%A7%81%EA%B3%B5%EC%8B%9D http://ko.wikipedia.org/wiki/스털링공식]
 
* [http://ko.wikipedia.org/wiki/%EC%8A%A4%ED%84%B8%EB%A7%81%EA%B3%B5%EC%8B%9D http://ko.wikipedia.org/wiki/스털링공식]
 
* [http://en.wikipedia.org/wiki/Stirling%27s http://en.wikipedia.org/wiki/Stirling's]
 
* [http://en.wikipedia.org/wiki/Stirling%27s http://en.wikipedia.org/wiki/Stirling's]
132번째 줄: 120번째 줄:
 
* [http://www.wolframalpha.com/input/?i=stirling%27s+formula http://www.wolframalpha.com/input/?i=stirling's+formula]
 
* [http://www.wolframalpha.com/input/?i=stirling%27s+formula http://www.wolframalpha.com/input/?i=stirling's+formula]
  
−
 
+
  
−
<h5>관련기사</h5>
+
  
−
*  네이버 뉴스 검색 (키워드 수정)<br>
+
==관련논문==
−
** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
 
−
** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
 
−
** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
 
−
** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
 
−
** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
 
  
−
 
+
  
−
 
+
* [http://www.jstor.org/stable/2324749 A New Derivation of Stirling's Approximation to n!]
−
 
+
** George Marsaglia and John C. W. Marsaglia, The American Mathematical Monthly, Vol. 97, No. 9 (Nov., 1990), pp. 826-829
−
<h5>블로그</h5>
 
−
 
 
−
* [http://gowers.wordpress.com/2008/02/01/removing-the-magic-from-stirlings-formula/ Removing the magic from Stirling’s formula]<br>
 
−
** Gowers’s Weblog
 
−
** 2008-2-1
 
−
 
 
−
* 구글 블로그 검색 http://blogsearch.google.com/blogsearch?q=
 
−
* 트렌비 블로그 검색 http://www.trenb.com/search.qst?q=
 
  
−
 
+
  
−
<h5>이미지 검색</h5>
+
  
−
* http://commons.wikimedia.org/w/index.php?title=Special%3ASearch&search=
+
−
* http://images.google.com/images?q=
 
−
* [http://www.artchive.com/ http://www.artchive.com]
 
  
−
 
+
==블로그==
  
−
<h5>동영상</h5>
+
* [http://gowers.wordpress.com/2008/02/01/removing-the-magic-from-stirlings-formula/ Removing the magic from Stirling’s formula]
 +
** Gowers’s Weblog, 2008-2-1
 +
[[분류:원주율]]
 +
[[분류:미적분학]]
  
−
* http://www.youtube.com/results?search_type=&search_query=
+
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q470877 Q470877]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'stirling'}, {'LOWER': "'s"}, {'LEMMA': 'approximation'}]
 +
* [{'LOWER': 'stirling'}, {'LOWER': "'s"}, {'LEMMA': 'formula'}]

2021년 2월 17일 (수) 04:50 기준 최신판

개요

  • 팩토리얼(factorial)의 근사식 \[ n! \approx \sqrt{2\pi n}\, \left(\frac{n}{e}\right)^{n}\]
  • 좀더 정확한 점근 급수(asymptotic series)는 다음과 같이 주어짐 \[ n!=\sqrt{2\pi n}\left({n\over e}\right)^n \left( 1 +{1\over12n} +{1\over288n^2} -{139\over51840n^3} -{571\over2488320n^4} + \cdots \right)\]

증명1 : 오일러-맥클로린 공식의 응용

  • 먼저 \(n!\) 에 로그를 취하여 덧셈형태로 쓴다\[\ln(n!)= \sum_{k = 0}^{n-1}\ln(1+k)\]
  • 이제 오일러-맥클로린 공식을 사용하자.

\[\sum_{i=0}^{n-1} f(i) = \sum_{k=0}^p\frac{B_k}{k!}\left(f^{(k-1)}(n)-f^{(k-1)}(0)\right)+R\]

  • 다시쓰면,

\[\sum_{i=0}^{n-1} f(i) = \int^n_0f(x)\,dx-\frac{1}{2}(f(n)-f(0))+\frac{1}{12}(f'(n)-f'(0))-\frac{1}{720}(f^{(3)}(n)-f^{(3)}(0))+\frac{1}{30240}(f^{(5)}(n)-f^{(5)}(0))-\frac{1}{1209600}(f^{(7)}(n)-f^{(7)}(0))+\cdots\]

  • 오차항은 다음과 같이 주어짐

\[\left|R\right|\leq\frac{2}{(2\pi)^{2(p+1)}}\int_0^n\left|f^{(p)}(x)\right|\,dx\]

  • \(f(x) = \ln(1+x)\) 에서 유도. \(R\) 은 0 으로 수렴한다.

\[f^{(k-1)}(x)=(-1)^{k-1}\frac{(k-1)!}{x^{k}}\] \[\frac{B_k}{k!}\left(f^{(k-1)}(n)-f^{(k-1)}(1)\right) =(-1)^{k-1}\frac{B_k}{k}(\frac{1}{n^{k}}-1)\] \[\int f(x)\,dx=(1+x)\ln (1+x)-x\] \[f(x)=\ln (1+x)\] \[f'(x)=\frac{1}{1+x}\] \[f^{(2)}(x)=\frac{-1}{(1+x)^2}\] \[f^{(3)}(x)=\frac{2}{(1+x)^3}\] \[f^{(4)}(x)=\frac{-6}{(1+x)^4}\] \[f^{(k-1)}(x)=(-1)^{k}\frac{(k-1)!}{x^{k-1}}\]

  • 위의 결과를 쓰면

\[\ln(n!)= \sum_{k = 0}^{n-1}\ln(1+k)=n\ln n - n-\frac{1}{2}\ln n+\frac{1}{12}(\frac{1}{n}-1)+\cdots\]

그러므로, \[ n! \approx B\sqrt{n}\, \left(\frac{n}{e}\right)^{n}\]

  • 계수 \(\sqrt{2 \pi}\) 는 어떻게 얻을까?

\[\frac{\pi}{2}=\lim_{n\to\infty}{1\over{2n}}\cdot{{2^{4n}\,(n!)^4}\over{((2n)!)^2}}\] \[\sqrt{\frac{\pi}{2}}=\lim_{n\to\infty}\sqrt{{1\over{2n}}}\cdot{{2^{2n}\,(n!)^2}\over{(2n)!}}=\lim_{n\to\infty}\sqrt{{1\over{2n}}}\cdot{{2^{2n}\,(B\sqrt{n}\, \left(\frac{n}{e}\right)^{n})^2}\over{B\sqrt{2n}\, \left(\frac{2n}{e}\right)^{2n}}}=\frac{B}{2}\] 따라서 \[B=\sqrt{2\pi}\]

증명2: 안장점 근사의 응용

  • 안장점 근사
  • 일반적으로 N이 클 때, 다음과 같은 근사식이 성립한다 \[\int e^{Nf(x)}\,dx\approx \sqrt{\frac{2\pi}{N|f''(x_0)|}}e^{Nf(x_0)}\textrm{ as }N\to\infty\] 최대값 부근에서의 테일러 전개 \(f(x)\approx f(x_0)-\frac{1}{2}|f''(x_0)|(x-x_0)^2\)를 이용
  • 스털링공식에의 적용


\(N! = \Gamma(N+1)=\int_0^{\infty} e^{-x} x^N dx\) 에서 \(x=Nz\) 로 치환하면,

\(N!= \int_0^{\infty} e^{-N z} \left(N z \right)^N N dz=N^{N+1}\int_0^{\infty}e^{N(\ln z-z)} dz\)

\(f \left( z \right) = \ln{z}-z\)

\(f'(z) = \frac{1}{z}-1\)

\(f''(z) = -\frac{1}{z^2}\)

\(z_0=1\) 일 때, 최대값을 가지며, \(f(z)\approx -1-\frac{1}{2} (z-1)^2+O[z-1]^3\) 가 된다.

따라서

\(N! \approx N^{N+1}\int_0^{\infty}e^{-N}e^{-\frac{N(z-1)^2}{2}} dz \approx N^{N+1}\sqrt{\frac{2\pi}{N}} e^{-N}=\sqrt{2\pi N} N^N e^{-N}\)


N=100일 때,

\(\sqrt{\frac{2\pi}{N}} e^{-N}\approx 9.33262\times 10^{-45}\)

\(\int_0^{\infty}e^{N(\ln z-z)} dz\approx 9.32485\times 10^{-45}\)


\(e^{N(\ln z-z)}\) 의 그래프 스털링 공식1.gif



재미있는 사실

  • 드무아브르가 스털링에 앞서서 팩토리얼의 근사식을 유도함.
  • 다만 \(\sqrt{2\pi}\)이라는 상수를 구하지 않고 적당한 상수 \(B\)에 대하여 다음과 수준의 표현을 남김.\[ n! \approx B\sqrt{n}\, \left(\frac{n}{e}\right)^{n}\]
  • 나중에 \(B=\sqrt{2\pi}\) 는 스털링이 해결함.

In Miscellanea Analytica (1730) appears Stirling’s formula (wrongly attributed to Stirling) which de Moivre used in 1733 to derive the normal curve as an approximation to the binomial. In the second edition of the book in 1738 de Moivre gives credit to Stirling for an improvement to the formula. De Moivre wrote:-

I desisted in proceeding farther till my worthy and learned friend Mr James Stirling, who had applied after me to that inquiry, [discovered that c = √(2 π)]. (http://www-groups.dcs.st-and.ac.uk/~history/Biographies/De_Moivre.html)

  • 오늘날 팩토리얼의 근사식은 선구적인 업적을 남긴 드무아브르의 이름은 온데간데 없이 스털링의 공식이라고 불리게 됨.
  • 드무아브르는 조금 섭섭하지 않을런지?
  • 팩토리얼은 정의는 간단할지라도 n이 조금만 커지기 시작하면 계산하기가 그리 만만치 않음. 실용적인 측면에서도 유용한 근사식.




관련된 항목들


매스매티카 파일 및 계산 리소스

수학용어번역

사전형태의 자료



관련논문




블로그

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'stirling'}, {'LOWER': "'s"}, {'LEMMA': 'approximation'}]
  • [{'LOWER': 'stirling'}, {'LOWER': "'s"}, {'LEMMA': 'formula'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=스털링_공식&oldid=52372"