"타원"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) (→노트: 새 문단) |
|||
| (사용자 3명의 중간 판 25개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | * 두 | + | * 원뿔의 단면에서 얻어지는 원뿔곡선의 하나 |
| − | + | * [[이차곡선(원뿔곡선)|이차곡선]]의 하나이다 | |
| − | ** | + | * 타원위의 점들은 어떤 두 점(초점)에서의 거리의 합이 일정하다 |
| − | ** | + | |
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | ==타원의 방정식== | ||
| + | |||
| + | * 타원은 이차곡선 <math>ax^2+bxy+cy^2+dx+ey+f=0</math>의 판별식이 <math>\Delta=b^2-4ac<0</math>인 경우 | ||
| + | * 타원의 방정식의 표준형 | ||
| + | ** <math>\frac{x^2}{a^2}+\frac{y^2}{b^2}=1</math> | ||
| + | ** <math>a=b</math> 이면 원이다. <math>a>b</math> 이면 가로( 축)로 납작한 타원, <math>a<b</math> 이면 세로로 길쭉한 타원이 된다. | ||
** 두 축 중 긴 것을 장축, 짧은 것을 단축이라 한다. | ** 두 축 중 긴 것을 장축, 짧은 것을 단축이라 한다. | ||
| − | + | * 평행이동, 회전변환에 의해서도 변형해도 여전히 타원이 얻어짐. | |
| + | |||
| + | |||
| + | |||
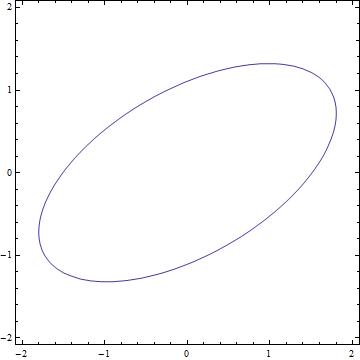
| + | [[파일:1999042-ellipse.jpg]] | ||
| + | |||
| + | <math>\frac{1}{4} \left(\frac{\sqrt{3} x}{2}+\frac{y}{2}\right)^2+\left(-\frac{x}{2}+\frac{\sqrt{3} y}{2}\right)^2=1</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==타원 둘레의 길이== | ||
| + | |||
| + | * [[타원 둘레의 길이]] 항목 참조 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==타원내부의 면적== | ||
| − | + | * 다음과 같이 주어진 타원 내부의 면적은 <math>\pi a b</math> 이다:<math>\frac{x^2}{a^2}+\frac{y^2}{b^2}\leq 1</math> | |
| + | * [[타원의 넓이]] 항목 참조 | ||
| + | |||
| − | + | ||
| − | + | ==배우기 전에 알고 있어야 하는 것들== | |
| − | * 다항식 | + | * 다항식 |
** 일차식과 이차식 | ** 일차식과 이차식 | ||
* 원의 방정식 | * 원의 방정식 | ||
| − | + | ||
| − | + | ||
| − | + | ==중요한 개념 및 정리== | |
| − | + | * 타원 <math>\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 (0<b<a)</math>을 고려하자. | |
| + | * 초점 <math>f=\sqrt{a^2-b^2}</math>라 두면, <math>(\pm f,0)</math> | ||
| + | * 이심률 (eccentricity) | ||
| + | ** 타원이 원에서 멀어지는 것을 재는 양 . 이심률은 <math>e=\frac{f}{a}=\frac{\sqrt{a^2-b^2}}{a}=\sqrt{1-\frac{b^2}{a^2}}</math>로 주어진다 | ||
| − | + | ==재미있는 문제== | |
| − | * | + | * 타원 <math>\frac{x^2}{a^2}+\frac{y^2}{b^2}=1</math> 에 외접하는 사각형의 최소 넓이는 |
* 빛의 반사성 : 한 초점에서 나온 빛은 타원 벽에서 반사되어 다른 초점으로 들어간다. | * 빛의 반사성 : 한 초점에서 나온 빛은 타원 벽에서 반사되어 다른 초점으로 들어간다. | ||
| − | * 매개변수표현 : | + | * 매개변수표현 |
| + | * 타원과 포물선 가 직교하기 위해서는 를 만족하면 된다. | ||
| + | ** [[파일:1999042-2.gif]] | ||
| − | + | ||
| + | ==관련된 항목들== | ||
| + | * [[타원내의 격자점 개수 문제]] | ||
| + | |||
| − | + | ===관련된 개념 및 나중에 더 배우게 되는 것들=== | |
| − | + | * [[타원과 인간]] | |
| + | * [[케플러의 법칙, 행성운동과 타원|행성운동과 타원]] | ||
| − | + | ||
| + | |||
| − | + | ===관련있는 다른 과목=== | |
| − | * 물리 | + | * 물리 |
** 행성운동 | ** 행성운동 | ||
** 지구는 태양의 주위를, 태양을 하나의 초점으로 하는 타원궤도로 돌고 있음. | ** 지구는 태양의 주위를, 태양을 하나의 초점으로 하는 타원궤도로 돌고 있음. | ||
| − | * 미술 | + | * 미술 |
** 원근법 | ** 원근법 | ||
** 원을 바르게 그리려면, 타원으로 그려야 함. | ** 원을 바르게 그리려면, 타원으로 그려야 함. | ||
| − | [ | + | [[파일:1999042-ellipse1.JPG]] |
| + | |||
| + | |||
| + | |||
| + | ===관련된 대학교 수학=== | ||
| − | + | * [[타원곡선]] | |
| + | * [[타원적분|타원적분, 타원함수, 타원곡선]] | ||
| − | + | ||
| − | + | ||
| − | + | ==블로그== | |
| − | + | * [http://bomber0.byus.net/index.php/2008/09/16/744 미적분과 인문계(3) : 타원 - 자연, 예술, 인간] (피타고라스의 창) | |
| − | |||
| − | + | [[분류:곡선]] | |
| + | [[분류:고교수학]] | ||
| − | + | == 노트 == | |
| − | * | + | * You see here, we're really, if we're on this point on the ellipse, we're really close to the origin.<ref name="ref_faa8">[https://www.khanacademy.org/math/precalculus/x9e81a4f98389efdf:conics/x9e81a4f98389efdf:ellipse-center-radii/v/conic-sections-intro-to-ellipses Intro to ellipses (video)]</ref> |
| − | ** | + | * And the way I drew this, we have kind of a short and fat ellipse you can also have kind of a tall and skinny ellipse.<ref name="ref_faa8" /> |
| + | * But in the short and fat ellipse, the direction that you're short in that's called your minor axis.<ref name="ref_faa8" /> | ||
| + | * If b was larger than a, I would have a tall and skinny ellipse.<ref name="ref_faa8" /> | ||
| + | * ; Description Draws an ellipse (oval) to the screen.<ref name="ref_e7df">[https://processing.org/reference/ellipse_.html ellipse() \ Language (API) \ Processing 3+]</ref> | ||
| + | * A straight line drawn through the foci and extended to the curve in either direction is the major diameter (or major axis) of the ellipse.<ref name="ref_8a82">[https://www.britannica.com/science/ellipse Ellipse | mathematics]</ref> | ||
| + | * This section focuses on the four variations of the standard form of the equation for the ellipse.<ref name="ref_463c">[https://courses.lumenlearning.com/waymakercollegealgebra/chapter/equations-of-ellipses/ Equations of Ellipses]</ref> | ||
| + | * We can draw an ellipse using a piece of cardboard, two thumbtacks, a pencil, and string.<ref name="ref_463c" /> | ||
| + | * Place the thumbtacks in the cardboard to form the foci of the ellipse.<ref name="ref_463c" /> | ||
| + | * The derivation of the standard form of the equation of an ellipse relies on this relationship and the distance formula.<ref name="ref_463c" /> | ||
| + | * Eccentricity is a number that describe the degree of roundness of the ellipse.<ref name="ref_b1b8">[http://xahlee.info/SpecialPlaneCurves_dir/Ellipse_dir/ellipse.html Ellipse]</ref> | ||
| + | * is the line segment passing the foci and intersects with the ellipse.<ref name="ref_b1b8" /> | ||
| + | * is the line segment perpendicular to the major axis, passing the center of foci, and intersects with the ellipse.<ref name="ref_b1b8" /> | ||
| + | * The formula for ellipse can be derived in many ways.<ref name="ref_b1b8" /> | ||
| + | * It is an ellipse! and draw a curve.<ref name="ref_e882">[https://www.mathsisfun.com/geometry/ellipse.html Ellipse]</ref> | ||
| + | * It goes from one side of the ellipse, through the center, to the other side, at the widest part of the ellipse.<ref name="ref_e882" /> | ||
| + | * Try bringing the two focus points together (so the ellipse is a circle) ...<ref name="ref_e882" /> | ||
| + | * An ellipse is the set of all points \((x,y)\) in a plane such that the sum of their distances from two fixed points is a constant.<ref name="ref_a6f7">[https://math.libretexts.org/Bookshelves/Algebra/Book%3A_Algebra_and_Trigonometry_(OpenStax)/12%3A_Analytic_Geometry/12.02%3A_The_Ellipse 12.2: The Ellipse]</ref> | ||
| + | * If \((a,0)\) is a vertex of the ellipse, the distance from \((−c,0)\) to \((a,0)\) is \(a−(−c)=a+c\).<ref name="ref_a6f7" /> | ||
| + | * It follows that \(d_1+d_2=2a\) for any point on the ellipse.<ref name="ref_a6f7" /> | ||
| + | * What is the standard form equation of the ellipse that has vertices \((\pm 8,0)\) and foci \((\pm 5,0)\)?<ref name="ref_a6f7" /> | ||
| + | * Populations of the ellipse are declining across the state, Inoue said.<ref name="ref_aa62">[https://www.merriam-webster.com/dictionary/ellipse Definition of Ellipse by Merriam-Webster]</ref> | ||
| + | * The storm will move into the right entrance region of the jet streak, shown by the large red ellipse.<ref name="ref_aa62" /> | ||
| + | * In other words, the orbit can be elliptical, but the ellipse can have any orientation in space.<ref name="ref_aa62" /> | ||
| + | * Supermoons occur because the moon orbits the Earth in the shape of an ellipse.<ref name="ref_aa62" /> | ||
| + | * In "primitive" geometrical terms, an ellipse is the figure you can draw in the sand by the following process: Push two sticks into the sand.<ref name="ref_30d9">[https://www.purplemath.com/modules/ellipse.htm Conics: Ellipses: Introduction]</ref> | ||
| + | * The resulting shape drawn in the sand is an ellipse.<ref name="ref_30d9" /> | ||
| + | * Each of the two sticks you first pushed into the sand is a " focus " of the ellipse; the two together are called "foci" (FOH-siy).<ref name="ref_30d9" /> | ||
| + | * The points where the major axis touches the ellipse are the " vertices " of the ellipse.<ref name="ref_30d9" /> | ||
| + | * An ellipse is the set of all points P in a plane such that the sum of the distances from P to two fixed points is a given constant.<ref name="ref_e596">[https://www.varsitytutors.com/hotmath/hotmath_help/topics/ellipse Ellipses]</ref> | ||
| + | * The center of the ellipse is the midpoint of the line segment joining its foci.<ref name="ref_e596" /> | ||
| + | * The major axis of the ellipse is the chord that passes through its foci and has its endpoints on the ellipse.<ref name="ref_e596" /> | ||
| + | * The graph of an ellipse can be translated so that its center is at the point ( h , k ) .<ref name="ref_e596" /> | ||
| + | * The ellipse is one of the four classic conic sections created by slicing a cone with a plane.<ref name="ref_13e3">[https://astronomy.swin.edu.au/cosmos/e/Ellipse Ellipse]</ref> | ||
| + | * The shape of the ellipse is described by its eccentricity.<ref name="ref_13e3" /> | ||
| + | * The larger the semi-major axis relative to the semi-minor axis, the more eccentric the ellipse is said to be.<ref name="ref_13e3" /> | ||
| + | * The equation of the ellipse can also be written in terms of the polar coordinates (r, f).<ref name="ref_13e3" /> | ||
| + | * The ellipse was first studied by Menaechmus Euclid wrote about the ellipse and it was given its present name by Apollonius .<ref name="ref_9f96">[https://mathshistory.st-andrews.ac.uk/Curves/Ellipse/ Ellipse]</ref> | ||
| + | * There is no exact formula for the length of an ellipse in elementary functions and this led to the study of elliptic functions.<ref name="ref_9f96" /> | ||
| + | * The evolute of the ellipse with equation given above is the Lamé curve.<ref name="ref_9f96" /> | ||
| + | * The ellipse is the set of all points R in the plane such that PR + QR is a fixed constant.<ref name="ref_d018">[http://ltcconline.net/greenl/courses/103b/Conics/ELLIPSE.HTM The Ellipse]</ref> | ||
| + | * An ellipse can be constructed using a piece of string.<ref name="ref_d018" /> | ||
| + | * Then with a pencil pull the string so that the string is tight and move the string around to form the ellipse.<ref name="ref_d018" /> | ||
| + | * This number tells us how squished the ellipse is.<ref name="ref_d018" /> | ||
| + | * In other words, the caustic by refraction of the ellipse for rays parallel to the axis reduces to the two foci.<ref name="ref_a615">[https://mathcurve.com/courbes2d.gb/ellipse/ellipse.shtml Ellipse]</ref> | ||
| + | * Conversely, the ellipse is the boundary of any convex set with oblique axes of symmetry in every direction.<ref name="ref_a615" /> | ||
| + | * An ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane, is constant.<ref name="ref_a163">[https://byjus.com/maths/ellipse/ Ellipse (Definition, Equation, Properties, Eccentricity, Formulas)]</ref> | ||
| + | * The shape of the ellipse is in an oval shape and the area of an ellipse is defined by its major axis and minor axis.<ref name="ref_a163" /> | ||
| + | * The ellipse is one of the conic sections, that is produced, when a plane cuts the cone at an angle with the base.<ref name="ref_a163" /> | ||
| + | * In geometry, an ellipse is a two-dimensional shape, that is defined along its axes.<ref name="ref_a163" /> | ||
| + | * An ellipse is the set of points in a plane such that the sum of the distances from two fixed points in that plane stays constant.<ref name="ref_0bd0">[https://www.cliffsnotes.com/study-guides/algebra/algebra-ii/conic-sections/ellipse Ellipse]</ref> | ||
| + | * The midpoint of the segment joining the foci is called the center of the ellipse.<ref name="ref_0bd0" /> | ||
| + | * When an ellipse is written in standard form, the major axis direction is determined by noting which variable has the larger denominator.<ref name="ref_0bd0" /> | ||
| + | * Graph the following ellipse.<ref name="ref_0bd0" /> | ||
| + | * We know that an ellipse is characterized by its squished circle or oval shape.<ref name="ref_f791">[https://www.superprof.co.uk/resources/academic/maths/analytical-geometry/conics/ellipse.html Superprof]</ref> | ||
| + | * An ellipse eccentricity measures how imperfectly round or squished an ellipse is.<ref name="ref_f791" /> | ||
| + | * As the foci of an ellipse are moved towards the center, the shape of the ellipse becomes closer to that of the circle.<ref name="ref_f791" /> | ||
| + | * If the foci of the ellipse are at the center, i.e. c = 0, then the value of eccentricity will become 0.<ref name="ref_f791" /> | ||
| + | * The set of all points in a plane, the sum of whose distances from two fixed points in the plane is constant is an ellipse.<ref name="ref_2f00">[https://www.toppr.com/guides/maths/conic-sections/equations-of-ellipse/ Ellipse: Definition, Equations, Derivations, Observations, Q&A]</ref> | ||
| + | * These two fixed points are the foci of the ellipse (Fig. 1).<ref name="ref_2f00" /> | ||
| + | * We know that both points P and Q are on the ellipse.<ref name="ref_2f00" /> | ||
| + | * Hence, the ellipse becomes a circle.<ref name="ref_2f00" /> | ||
| + | * An ellipse is a circle that has been stretched in one direction, to give it the shape of an oval.<ref name="ref_cb0d">[https://www.maa.org/external_archive/joma/Volume8/Kalman/Ellipse1.html The Most Marvelous Theorem in Mathematics]</ref> | ||
| + | * But not every oval is an ellipse, as shown in Figure 1, below.<ref name="ref_cb0d" /> | ||
| + | * There is a specific kind of stretching that turns a circle into an ellipse, as we shall see on the next page.<ref name="ref_cb0d" /> | ||
| + | * Figure 2 hints at the nature of the type of stretching that creates an ellipse.<ref name="ref_cb0d" /> | ||
| + | * The major axis is the segment that contains both foci and has its endpoints on the ellipse.<ref name="ref_a624">[https://www.mathwarehouse.com/ellipse/equation-of-ellipse.php Equation of an Ellipse in Standard Form and how it relates to the graph of the Ellipse.]</ref> | ||
| + | * An ellipse looks like a circle that has been squashed into an oval.<ref name="ref_4f87">[https://www.mathopenref.com/ellipse.html math word definition- Math Open Reference]</ref> | ||
| + | * An ellipse is defined by two points, each called a focus.<ref name="ref_4f87" /> | ||
| + | * If you take any point on the ellipse, the sum of the distances to the focus points is constant.<ref name="ref_4f87" /> | ||
| + | * In the figure above, drag the point on the ellipse around and see that while the distances to the focus points vary, their sum is constant.<ref name="ref_4f87" /> | ||
| + | * The term ellipse has been coined by Apollonius of Perga, with a connotation of being "left out".<ref name="ref_16b9">[https://www.cut-the-knot.org/WhatIs/WhatIsEllipse.shtml What Is Ellipse?]</ref> | ||
| + | * There are many ways to define an ellipse.<ref name="ref_16b9" /> | ||
| + | * We cite several common definitions, prove that all are equivalent, and, based on these, derive additional properties of ellipse.<ref name="ref_16b9" /> | ||
| + | * The ellipse touches the sides at the points (± a 1 ± a 2 cos δ) and (± a 1 cos δ, ± a 2 ).<ref name="ref_5d51">[https://www.sciencedirect.com/topics/mathematics/ellipse Ellipse - an overview]</ref> | ||
| + | * We distinguish two cases of polarization, according to the sense in which the end point of the electric vector describes the ellipse.<ref name="ref_5d51" /> | ||
| + | * F2 are called the foci of the ellipse (singular: focus).<ref name="ref_1950">[https://brilliant.org/wiki/conics-ellipse-general/ Brilliant Math & Science Wiki]</ref> | ||
| + | * F2 is called the major axis of the ellipse, and the axis perpendicular to the major axis is the minor axis.<ref name="ref_1950" /> | ||
| + | * A tunnel opening is shaped like a half ellipse.<ref name="ref_1950" /> | ||
| + | * Find the equation of the ellipse assuming it is centered at the origin.<ref name="ref_1950" /> | ||
| + | * is the line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is at a minimum.<ref name="ref_286f">[https://saylordotorg.github.io/text_intermediate-algebra/s11-03-ellipses.html Ellipses]</ref> | ||
| + | * If the major axis of an ellipse is parallel to the x-axis in a rectangular coordinate plane, we say that the ellipse is horizontal.<ref name="ref_286f" /> | ||
| + | * If the major axis is parallel to the y-axis, we say that the ellipse is vertical.<ref name="ref_286f" /> | ||
| + | * However, the ellipse has many real-world applications and further research on this rich subject is encouraged.<ref name="ref_286f" /> | ||
| + | * As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same.<ref name="ref_1b3a">[https://en.wikipedia.org/wiki/Ellipse Wikipedia]</ref> | ||
| + | * The midpoint C {\displaystyle C} of the line segment joining the foci is called the center of the ellipse.<ref name="ref_1b3a" /> | ||
| + | * An arbitrary line g {\displaystyle g} intersects an ellipse at 0, 1, or 2 points, respectively called an exterior line, tangent and secant.<ref name="ref_1b3a" /> | ||
| + | * \displaystyle w} which is different from P {\displaystyle P} cannot be on the ellipse.<ref name="ref_1b3a" /> | ||
| + | * Click on the blue point on the ellipse and drag it to change the figure.<ref name="ref_345a">[http://lifeisastoryproblem.tripod.com/en/e/ellipse.html Ellipse: A closed curve with an equation in the form (x-h)^2/a+-(y-k)^2/b=1.]</ref> | ||
| + | * The eccentricity of an ellipse is a measure of how much it is changed from a circle.<ref name="ref_345a" /> | ||
| + | * The ellipse was first studied by Menaechmus, investigated by Euclid, and named by Apollonius.<ref name="ref_c9aa">[https://mathworld.wolfram.com/Ellipse.html Ellipse -- from Wolfram MathWorld]</ref> | ||
| + | * The focus and conic section directrix of an ellipse were considered by Pappus.<ref name="ref_c9aa" /> | ||
| + | * In 1602, Kepler believed that the orbit of Mars was oval; he later discovered that it was an ellipse with the Sun at one focus.<ref name="ref_c9aa" /> | ||
| + | * Let an ellipse lie along the x-axis and find the equation of the figure (1) where and are at and .<ref name="ref_c9aa" /> | ||
| + | ===소스=== | ||
| + | <references /> | ||
2020년 12월 17일 (목) 01:51 기준 최신판
개요
- 원뿔의 단면에서 얻어지는 원뿔곡선의 하나
- 이차곡선의 하나이다
- 타원위의 점들은 어떤 두 점(초점)에서의 거리의 합이 일정하다
타원의 방정식
- 타원은 이차곡선 \(ax^2+bxy+cy^2+dx+ey+f=0\)의 판별식이 \(\Delta=b^2-4ac<0\)인 경우
- 타원의 방정식의 표준형
- \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
- \(a=b\) 이면 원이다. \(a>b\) 이면 가로( 축)로 납작한 타원, \(a<b\) 이면 세로로 길쭉한 타원이 된다.
- 두 축 중 긴 것을 장축, 짧은 것을 단축이라 한다.
- 평행이동, 회전변환에 의해서도 변형해도 여전히 타원이 얻어짐.
\(\frac{1}{4} \left(\frac{\sqrt{3} x}{2}+\frac{y}{2}\right)^2+\left(-\frac{x}{2}+\frac{\sqrt{3} y}{2}\right)^2=1\)
타원 둘레의 길이
- 타원 둘레의 길이 항목 참조
타원내부의 면적
- 다음과 같이 주어진 타원 내부의 면적은 \(\pi a b\) 이다\[\frac{x^2}{a^2}+\frac{y^2}{b^2}\leq 1\]
- 타원의 넓이 항목 참조
배우기 전에 알고 있어야 하는 것들
- 다항식
- 일차식과 이차식
- 원의 방정식
중요한 개념 및 정리
- 타원 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 (0<b<a)\)을 고려하자.
- 초점 \(f=\sqrt{a^2-b^2}\)라 두면, \((\pm f,0)\)
- 이심률 (eccentricity)
- 타원이 원에서 멀어지는 것을 재는 양 . 이심률은 \(e=\frac{f}{a}=\frac{\sqrt{a^2-b^2}}{a}=\sqrt{1-\frac{b^2}{a^2}}\)로 주어진다
재미있는 문제
- 타원 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) 에 외접하는 사각형의 최소 넓이는
- 빛의 반사성 : 한 초점에서 나온 빛은 타원 벽에서 반사되어 다른 초점으로 들어간다.
- 매개변수표현
- 타원과 포물선 가 직교하기 위해서는 를 만족하면 된다.
관련된 항목들
관련된 개념 및 나중에 더 배우게 되는 것들
관련있는 다른 과목
- 물리
- 행성운동
- 지구는 태양의 주위를, 태양을 하나의 초점으로 하는 타원궤도로 돌고 있음.
- 미술
- 원근법
- 원을 바르게 그리려면, 타원으로 그려야 함.
관련된 대학교 수학
블로그
- 미적분과 인문계(3) : 타원 - 자연, 예술, 인간 (피타고라스의 창)
노트
- You see here, we're really, if we're on this point on the ellipse, we're really close to the origin.[1]
- And the way I drew this, we have kind of a short and fat ellipse you can also have kind of a tall and skinny ellipse.[1]
- But in the short and fat ellipse, the direction that you're short in that's called your minor axis.[1]
- If b was larger than a, I would have a tall and skinny ellipse.[1]
- ; Description Draws an ellipse (oval) to the screen.[2]
- A straight line drawn through the foci and extended to the curve in either direction is the major diameter (or major axis) of the ellipse.[3]
- This section focuses on the four variations of the standard form of the equation for the ellipse.[4]
- We can draw an ellipse using a piece of cardboard, two thumbtacks, a pencil, and string.[4]
- Place the thumbtacks in the cardboard to form the foci of the ellipse.[4]
- The derivation of the standard form of the equation of an ellipse relies on this relationship and the distance formula.[4]
- Eccentricity is a number that describe the degree of roundness of the ellipse.[5]
- is the line segment passing the foci and intersects with the ellipse.[5]
- is the line segment perpendicular to the major axis, passing the center of foci, and intersects with the ellipse.[5]
- The formula for ellipse can be derived in many ways.[5]
- It is an ellipse! and draw a curve.[6]
- It goes from one side of the ellipse, through the center, to the other side, at the widest part of the ellipse.[6]
- Try bringing the two focus points together (so the ellipse is a circle) ...[6]
- An ellipse is the set of all points \((x,y)\) in a plane such that the sum of their distances from two fixed points is a constant.[7]
- If \((a,0)\) is a vertex of the ellipse, the distance from \((−c,0)\) to \((a,0)\) is \(a−(−c)=a+c\).[7]
- It follows that \(d_1+d_2=2a\) for any point on the ellipse.[7]
- What is the standard form equation of the ellipse that has vertices \((\pm 8,0)\) and foci \((\pm 5,0)\)?[7]
- Populations of the ellipse are declining across the state, Inoue said.[8]
- The storm will move into the right entrance region of the jet streak, shown by the large red ellipse.[8]
- In other words, the orbit can be elliptical, but the ellipse can have any orientation in space.[8]
- Supermoons occur because the moon orbits the Earth in the shape of an ellipse.[8]
- In "primitive" geometrical terms, an ellipse is the figure you can draw in the sand by the following process: Push two sticks into the sand.[9]
- The resulting shape drawn in the sand is an ellipse.[9]
- Each of the two sticks you first pushed into the sand is a " focus " of the ellipse; the two together are called "foci" (FOH-siy).[9]
- The points where the major axis touches the ellipse are the " vertices " of the ellipse.[9]
- An ellipse is the set of all points P in a plane such that the sum of the distances from P to two fixed points is a given constant.[10]
- The center of the ellipse is the midpoint of the line segment joining its foci.[10]
- The major axis of the ellipse is the chord that passes through its foci and has its endpoints on the ellipse.[10]
- The graph of an ellipse can be translated so that its center is at the point ( h , k ) .[10]
- The ellipse is one of the four classic conic sections created by slicing a cone with a plane.[11]
- The shape of the ellipse is described by its eccentricity.[11]
- The larger the semi-major axis relative to the semi-minor axis, the more eccentric the ellipse is said to be.[11]
- The equation of the ellipse can also be written in terms of the polar coordinates (r, f).[11]
- The ellipse was first studied by Menaechmus Euclid wrote about the ellipse and it was given its present name by Apollonius .[12]
- There is no exact formula for the length of an ellipse in elementary functions and this led to the study of elliptic functions.[12]
- The evolute of the ellipse with equation given above is the Lamé curve.[12]
- The ellipse is the set of all points R in the plane such that PR + QR is a fixed constant.[13]
- An ellipse can be constructed using a piece of string.[13]
- Then with a pencil pull the string so that the string is tight and move the string around to form the ellipse.[13]
- This number tells us how squished the ellipse is.[13]
- In other words, the caustic by refraction of the ellipse for rays parallel to the axis reduces to the two foci.[14]
- Conversely, the ellipse is the boundary of any convex set with oblique axes of symmetry in every direction.[14]
- An ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane, is constant.[15]
- The shape of the ellipse is in an oval shape and the area of an ellipse is defined by its major axis and minor axis.[15]
- The ellipse is one of the conic sections, that is produced, when a plane cuts the cone at an angle with the base.[15]
- In geometry, an ellipse is a two-dimensional shape, that is defined along its axes.[15]
- An ellipse is the set of points in a plane such that the sum of the distances from two fixed points in that plane stays constant.[16]
- The midpoint of the segment joining the foci is called the center of the ellipse.[16]
- When an ellipse is written in standard form, the major axis direction is determined by noting which variable has the larger denominator.[16]
- Graph the following ellipse.[16]
- We know that an ellipse is characterized by its squished circle or oval shape.[17]
- An ellipse eccentricity measures how imperfectly round or squished an ellipse is.[17]
- As the foci of an ellipse are moved towards the center, the shape of the ellipse becomes closer to that of the circle.[17]
- If the foci of the ellipse are at the center, i.e. c = 0, then the value of eccentricity will become 0.[17]
- The set of all points in a plane, the sum of whose distances from two fixed points in the plane is constant is an ellipse.[18]
- These two fixed points are the foci of the ellipse (Fig. 1).[18]
- We know that both points P and Q are on the ellipse.[18]
- Hence, the ellipse becomes a circle.[18]
- An ellipse is a circle that has been stretched in one direction, to give it the shape of an oval.[19]
- But not every oval is an ellipse, as shown in Figure 1, below.[19]
- There is a specific kind of stretching that turns a circle into an ellipse, as we shall see on the next page.[19]
- Figure 2 hints at the nature of the type of stretching that creates an ellipse.[19]
- The major axis is the segment that contains both foci and has its endpoints on the ellipse.[20]
- An ellipse looks like a circle that has been squashed into an oval.[21]
- An ellipse is defined by two points, each called a focus.[21]
- If you take any point on the ellipse, the sum of the distances to the focus points is constant.[21]
- In the figure above, drag the point on the ellipse around and see that while the distances to the focus points vary, their sum is constant.[21]
- The term ellipse has been coined by Apollonius of Perga, with a connotation of being "left out".[22]
- There are many ways to define an ellipse.[22]
- We cite several common definitions, prove that all are equivalent, and, based on these, derive additional properties of ellipse.[22]
- The ellipse touches the sides at the points (± a 1 ± a 2 cos δ) and (± a 1 cos δ, ± a 2 ).[23]
- We distinguish two cases of polarization, according to the sense in which the end point of the electric vector describes the ellipse.[23]
- F2 are called the foci of the ellipse (singular: focus).[24]
- F2 is called the major axis of the ellipse, and the axis perpendicular to the major axis is the minor axis.[24]
- A tunnel opening is shaped like a half ellipse.[24]
- Find the equation of the ellipse assuming it is centered at the origin.[24]
- is the line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is at a minimum.[25]
- If the major axis of an ellipse is parallel to the x-axis in a rectangular coordinate plane, we say that the ellipse is horizontal.[25]
- If the major axis is parallel to the y-axis, we say that the ellipse is vertical.[25]
- However, the ellipse has many real-world applications and further research on this rich subject is encouraged.[25]
- As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same.[26]
- The midpoint C {\displaystyle C} of the line segment joining the foci is called the center of the ellipse.[26]
- An arbitrary line g {\displaystyle g} intersects an ellipse at 0, 1, or 2 points, respectively called an exterior line, tangent and secant.[26]
- \displaystyle w} which is different from P {\displaystyle P} cannot be on the ellipse.[26]
- Click on the blue point on the ellipse and drag it to change the figure.[27]
- The eccentricity of an ellipse is a measure of how much it is changed from a circle.[27]
- The ellipse was first studied by Menaechmus, investigated by Euclid, and named by Apollonius.[28]
- The focus and conic section directrix of an ellipse were considered by Pappus.[28]
- In 1602, Kepler believed that the orbit of Mars was oval; he later discovered that it was an ellipse with the Sun at one focus.[28]
- Let an ellipse lie along the x-axis and find the equation of the figure (1) where and are at and .[28]
소스
- ↑ 1.0 1.1 1.2 1.3 Intro to ellipses (video)
- ↑ ellipse() \ Language (API) \ Processing 3+
- ↑ Ellipse | mathematics
- ↑ 4.0 4.1 4.2 4.3 Equations of Ellipses
- ↑ 5.0 5.1 5.2 5.3 Ellipse
- ↑ 6.0 6.1 6.2 Ellipse
- ↑ 7.0 7.1 7.2 7.3 12.2: The Ellipse
- ↑ 8.0 8.1 8.2 8.3 Definition of Ellipse by Merriam-Webster
- ↑ 9.0 9.1 9.2 9.3 Conics: Ellipses: Introduction
- ↑ 10.0 10.1 10.2 10.3 Ellipses
- ↑ 11.0 11.1 11.2 11.3 Ellipse
- ↑ 12.0 12.1 12.2 Ellipse
- ↑ 13.0 13.1 13.2 13.3 The Ellipse
- ↑ 14.0 14.1 Ellipse
- ↑ 15.0 15.1 15.2 15.3 Ellipse (Definition, Equation, Properties, Eccentricity, Formulas)
- ↑ 16.0 16.1 16.2 16.3 Ellipse
- ↑ 17.0 17.1 17.2 17.3 Superprof
- ↑ 18.0 18.1 18.2 18.3 Ellipse: Definition, Equations, Derivations, Observations, Q&A
- ↑ 19.0 19.1 19.2 19.3 The Most Marvelous Theorem in Mathematics
- ↑ Equation of an Ellipse in Standard Form and how it relates to the graph of the Ellipse.
- ↑ 21.0 21.1 21.2 21.3 math word definition- Math Open Reference
- ↑ 22.0 22.1 22.2 What Is Ellipse?
- ↑ 23.0 23.1 Ellipse - an overview
- ↑ 24.0 24.1 24.2 24.3 Brilliant Math & Science Wiki
- ↑ 25.0 25.1 25.2 25.3 Ellipses
- ↑ 26.0 26.1 26.2 26.3 Wikipedia
- ↑ 27.0 27.1 Ellipse: A closed curve with an equation in the form (x-h)^2/a+-(y-k)^2/b=1.
- ↑ 28.0 28.1 28.2 28.3 Ellipse -- from Wolfram MathWorld