"사토-테이트 추측 (Sato–Tate conjecture)"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) (→노트: 새 문단) |
||
| 84번째 줄: | 84번째 줄: | ||
===Spacy 패턴 목록=== | ===Spacy 패턴 목록=== | ||
* [{'LOWER': 'sato'}, {'OP': '*'}, {'LOWER': 'tate'}, {'LEMMA': 'conjecture'}] | * [{'LOWER': 'sato'}, {'OP': '*'}, {'LOWER': 'tate'}, {'LEMMA': 'conjecture'}] | ||
| + | |||
| + | == 노트 == | ||
| + | |||
| + | ===말뭉치=== | ||
| + | # The Sato-Tate conjecture Suppose E does not have CM.<ref name="ref_24243eeb">[https://kskedlaya.org/slides/vantage2020-handout.pdf The sato-tate conjecture and its generalizations]</ref> | ||
| + | # 13 / 33 A generalized Sato-Tate conjecture L-polynomials of algebraic varieties Let X be a smooth proper variety over K .<ref name="ref_24243eeb" /> | ||
| + | # In order to build a strategy towards proving the Sato-Tate conjecture, we quickly review the method of moments from Probability Theory.<ref name="ref_74facb5b">[https://www.math.mcgill.ca/darmon/courses/17-18/sato-tate/dimitris.pdf Notes on the sato-tate conjecture]</ref> | ||
| + | # In any NOTES ON THE SATO-TATE CONJECTURE 5 case, cj = 1.<ref name="ref_74facb5b" /> | ||
| + | # We prove the Sato-Tate conjecture for Hilbert modular forms.<ref name="ref_42cc7e13">[https://www.ams.org/jams/2011-24-02/S0894-0347-2010-00689-3/ AMS :: Journal of the American Mathematical Society]</ref> | ||
| + | # In Section 2, the generalized Sato Tate conjecture for arithmetic curves will be reviewed as the main mathematical background for this paper.<ref name="ref_e45ebedf">[https://www2.math.uconn.edu/~khlee/Papers/ML-STconj.pdf Machine-learning the sato–tate conjecture]</ref> | ||
| + | # To achieve this, under the same hypotheses, we prove an explicit version of the Sato–Tate conjecture for primes in arithmetic progressions.<ref name="ref_173b3f00">[https://www.worldscientific.com/doi/10.1142/S179304212150069X The explicit Sato–Tate conjecture for primes in arithmetic progressions]</ref> | ||
| + | # This report nevertheless begins with an introduction to Langlands reciprocity conjectures, and their arithmetic variants, in the situation most relevant to the proof of the Sato-Tate conjecture.<ref name="ref_aeaa5ecd">[https://webusers.imj-prg.fr/~michael.harris/SatoTate/notes/Introduction.pdf The sato-tate conjecture:]</ref> | ||
| + | # The main goal of this talk is to present new results in the direction of the algebraic Sato-Tate conjecture, building on the previous work of Serre, Kedlaya and Banaszak.<ref name="ref_ad0c2718">[https://indico.ictp.it/event/8941/ On an algebraic Sato-Tate conjecture for abelian varieties (27 May 2019)]</ref> | ||
| + | # Our observations are in keeping with the Sato-Tate conjecture for curves of low genus.<ref name="ref_0a8c9aad">[https://dl.acm.org/doi/10.1016/j.jsc.2021.11.002 Machine-learning the Sato–Tate conjecture]</ref> | ||
| + | # The Sato-Tate conjecture, in its rst formulation, concerns elliptic curves.<ref name="ref_a18e81ba">[https://staff.fnwi.uva.nl/l.d.j.taelman/pagani.pdf Master’s thesis in mathematics]</ref> | ||
| + | # Various people have asked me for an update on the status of the Sato-Tate conjecture for abelian surfaces in light of recent advances in modularity lifting theorems.<ref name="ref_094e435a">[https://www.galoisrepresentations.com/2018/07/19/update-on-sato-tate-for-abelian-surfaces/ Update on Sato-Tate for abelian surfaces]</ref> | ||
| + | # Case 2: The Sato-Tate conjecture is proved in this case.<ref name="ref_094e435a" /> | ||
| + | # Note that since the Sato-Tate conjecture is known in all other cases, one only has to consider cases (3) and (4), which behave slightly differently in this argument.<ref name="ref_094e435a" /> | ||
| + | # Bounded, Borel measurable R-valued central functions g on U Sp(4) are in one-one correspondence with bounded, Borel ON THE SATO-TATE CONJECTURE FOR GENUS TWO CURVES 3 Figure 1.<ref name="ref_5d17868c">[https://users.nber.org/~nroussan/satotate/satotate.pdf On the sato-tate conjecture for genus two]</ref> | ||
| + | ===소스=== | ||
| + | <references /> | ||
2022년 8월 24일 (수) 00:04 판
개요
- 유리수 체 위에 정의된 타원곡선 \(E\)를 생각하자
- 소수 \(p\)에 대하여 \(E(\mathbb{F}_p)\)의 원소의 개수를 \(M_p\)라 두고, \(\theta_p\)를 다음과 같이 정의하자
\[p+1-M_p=2\sqrt{p}\cos{\theta_p},\quad (0\leq \theta_p \leq \pi).\]
- 추측 (사토-테이트)
\(E\)가 complex multiplication을 갖지 않을 때, \(0\leq \alpha< \beta\leq \pi\)인 두 실수 \(\alpha, \beta\)에 대하여, 다음이 성립한다 \[\lim_{N\to\infty}\frac{\#\{p\leq N:\alpha\leq \theta_p \leq \beta\}} {\#\{p\leq N\}}=\frac{2}{\pi} \int_{\alpha}^{\beta} \sin^2 \theta \, d\theta. \]
예
- 타원곡선 \(y^2=x^3 + x + 1\)
- \(a_p=p+1-M_p\)라 두면, 다음과 같은 테이블을 얻는다
\[ \begin{array}{c|cc} p & a_p & \theta _p \\ \hline 2 & -2 & 2.35619 \\ 3 & 0 & 1.5708 \\ 5 & -3 & 2.30611 \\ 7 & 3 & 0.968002 \\ 11 & -2 & 1.87707 \\ 13 & -4 & 2.1588 \\ 17 & 0 & 1.5708 \\ 19 & -1 & 1.68576 \\ 23 & -4 & 2.00097 \\ 29 & -6 & 2.16167 \\ 31 & -1 & 1.66072 \\ 37 & -10 & 2.5357 \\ 41 & 7 & 0.992488 \\ 43 & 10 & 0.703639 \\ 47 & -12 & 2.63662 \\ 53 & -4 & 1.8491 \\ 59 & -3 & 1.76734 \\ 61 & 12 & 0.694738 \\ 67 & 12 & 0.74805 \\ 71 & 13 & 0.689745 \\ \end{array} \]
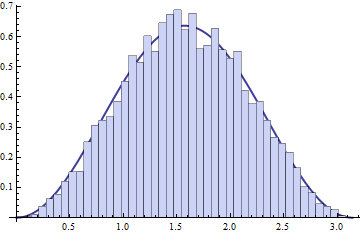
- 처음 5000개의 소수 \(p\)에 대하여, \(\theta_p\)의 분포는 다음과 같다
- 함께 그려진 곡선은 \(\frac{2}{\pi}\sin^2 \theta\)의 그래프
메모
- Lario, Joan-C., and Anna Somoza. “The Sato-Tate Conjecture for a Picard Curve with Complex Multiplication,” September 21, 2014. http://xxx.tau.ac.il/abs/1409.6020.
관련된 항목들
매스매티카 파일 및 계산 리소스
사전 형태의 자료
리뷰, 에세이, 강의노트
- Fité, Francesc. 2014. “Equidistribution, L-Functions, and Sato-Tate Groups.” arXiv:1405.5162 [math], May. http://arxiv.org/abs/1405.5162.
관련논문
- Yih-Dar Shieh, Character theory approach to Sato-Tate groups, arXiv:1605.07743 [math.NT], May 25 2016, http://arxiv.org/abs/1605.07743
- Henry H. Kim, Satoshi Wakatsuki, Takuya Yamauchi, An equidistribution theorem for holomorphic Siegel modular forms for \(GSp_4\), arXiv:1604.02036[math.NT], April 07 2016, http://arxiv.org/abs/1604.02036v1
- Jasmin Matz, Nicolas Templier, Sato-Tate equidistribution for families of Hecke-Maass forms on SL(n,R)/SO(n), http://arxiv.org/abs/1505.07285v3
- Sha, Min, and Igor E. Shparlinski. “The Sato--Tate Distribution in Families of Elliptic Curves with a Rational Parameter of Bounded Height.” arXiv:1512.07301 [math], December 22, 2015. http://arxiv.org/abs/1512.07301.
- Boyer, Pascal. “Lowering the Level and Ihara’s Lemma for Some Unitary Groups.” arXiv:1511.00144 [math], October 31, 2015. http://arxiv.org/abs/1511.00144.
- Sha, Min, Igor E. Shparlinski, and José Felipe Voloch. “The Sato-Tate Distribution in Thin Parametric Families of Elliptic Curves.” arXiv:1509.03009 [math], September 10, 2015. http://arxiv.org/abs/1509.03009.
- Chen, Evan, Peter S. Park, and Ashvin A. Swaminathan. ‘Linnik’s Theorem for Sato-Tate Laws on Elliptic Curves with Complex Multiplication’. arXiv:1506.09170 [math], 30 June 2015. http://arxiv.org/abs/1506.09170.
- Bucur, Alina, and Kiran S. Kedlaya. “An Application of the Effective Sato-Tate Conjecture.” arXiv:1301.0139 [math], January 1, 2013. http://arxiv.org/abs/1301.0139.
- Matz, Jasmin, and Nicolas Templier. ‘Sato-Tate Equidistribution for Families of Hecke-Maass Forms on SL(n,R)/SO(n)’. arXiv:1505.07285 [math], 27 May 2015. http://arxiv.org/abs/1505.07285.
- Thorner, Jesse. 2014. “The Error Term in the Sato-Tate Conjecture.” arXiv:1407.2656 [math], July. http://arxiv.org/abs/1407.2656.
- Barnet-Lamb, Tom, et al. "A family of Calabi-Yau varieties and potential automorphy II." Publ. Res. Inst. Math. Sci 47.1 (2011): 29-98.
- Harris, Michael, Nick Shepherd-Barron, and Richard Taylor. "A family of Calabi-Yau varieties and potential automorphy." Ann. of Math.(2) 171.2 (2010): 779-813.
메타데이터
위키데이터
- ID : Q2993331
Spacy 패턴 목록
- [{'LOWER': 'sato'}, {'OP': '*'}, {'LOWER': 'tate'}, {'LEMMA': 'conjecture'}]
노트
말뭉치
- The Sato-Tate conjecture Suppose E does not have CM.[1]
- 13 / 33 A generalized Sato-Tate conjecture L-polynomials of algebraic varieties Let X be a smooth proper variety over K .[1]
- In order to build a strategy towards proving the Sato-Tate conjecture, we quickly review the method of moments from Probability Theory.[2]
- In any NOTES ON THE SATO-TATE CONJECTURE 5 case, cj = 1.[2]
- We prove the Sato-Tate conjecture for Hilbert modular forms.[3]
- In Section 2, the generalized Sato Tate conjecture for arithmetic curves will be reviewed as the main mathematical background for this paper.[4]
- To achieve this, under the same hypotheses, we prove an explicit version of the Sato–Tate conjecture for primes in arithmetic progressions.[5]
- This report nevertheless begins with an introduction to Langlands reciprocity conjectures, and their arithmetic variants, in the situation most relevant to the proof of the Sato-Tate conjecture.[6]
- The main goal of this talk is to present new results in the direction of the algebraic Sato-Tate conjecture, building on the previous work of Serre, Kedlaya and Banaszak.[7]
- Our observations are in keeping with the Sato-Tate conjecture for curves of low genus.[8]
- The Sato-Tate conjecture, in its rst formulation, concerns elliptic curves.[9]
- Various people have asked me for an update on the status of the Sato-Tate conjecture for abelian surfaces in light of recent advances in modularity lifting theorems.[10]
- Case 2: The Sato-Tate conjecture is proved in this case.[10]
- Note that since the Sato-Tate conjecture is known in all other cases, one only has to consider cases (3) and (4), which behave slightly differently in this argument.[10]
- Bounded, Borel measurable R-valued central functions g on U Sp(4) are in one-one correspondence with bounded, Borel ON THE SATO-TATE CONJECTURE FOR GENUS TWO CURVES 3 Figure 1.[11]
소스
- ↑ 1.0 1.1 The sato-tate conjecture and its generalizations
- ↑ 2.0 2.1 Notes on the sato-tate conjecture
- ↑ AMS :: Journal of the American Mathematical Society
- ↑ Machine-learning the sato–tate conjecture
- ↑ The explicit Sato–Tate conjecture for primes in arithmetic progressions
- ↑ The sato-tate conjecture:
- ↑ On an algebraic Sato-Tate conjecture for abelian varieties (27 May 2019)
- ↑ Machine-learning the Sato–Tate conjecture
- ↑ Master’s thesis in mathematics
- ↑ 10.0 10.1 10.2 Update on Sato-Tate for abelian surfaces
- ↑ On the sato-tate conjecture for genus two